如图，椭圆Q：
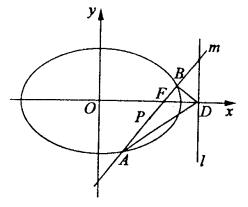
(1)求点P的轨迹H的方程；
(2)若在Q的方程中，令a2=1+cosθ+sinθ，b2=sinθ(0＜θ≤
设轨迹H的最高点和最低点分别为M和N.当θ为何值时，△MNF为—个正三角形?
如图，椭圆Q：
(1)求点P的轨迹H的方程；
(2)若在Q的方程中，令a2=1+cosθ+sinθ，b2=sinθ(0＜θ≤
设轨迹H的最高点和最低点分别为M和N.当θ为何值时，△MNF为—个正三角形?
如图，
（1）设椭圆Q：
由①-②得
b2(x1-x2)2x+a2(y1-y2)2y=0.
1°当AB不垂直x轴时，x1≠x2
得到
b2x2+a2y2-b2cx=0……（*）
2°当AB垂直于x轴时，点P即为点F，满足方程（*）
所以点P的轨迹H的方程为：b2x2+a2y2-b2cx=0
（2）因为轨迹H的方程可化为：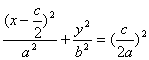
∴M（
），F(c，0)，使△MNF为一个正三角形时，
则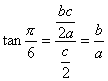
由于a2=1+cosθ+sinθ，b2=sinθ(0＜θ≤
)，
则1+cosθ+sinθ=3sinθ，得θ=2arctan
).