如图，D、E分别为△ABC的边AB、AC上的点，△ACD与△BCD的周长相等，△ABE与△CBE的周长相等，记△ABC的面积为S．若∠ACB=90°，则AD•CE与S的大小关系为（ ）
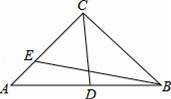
A．S=AD•CE B．S＞AD•CE C．S＜AD•CE D．无法确定
如图，D、E分别为△ABC的边AB、AC上的点，△ACD与△BCD的周长相等，△ABE与△CBE的周长相等，记△ABC的面积为S．若∠ACB=90°，则AD•CE与S的大小关系为（ ）
A．S=AD•CE B．S＞AD•CE C．S＜AD•CE D．无法确定
A【考点】勾股定理；三角形的面积．
【专题】计算题．
【分析】根据△BCD与△ACD的周长相等，我们可得出：BC+BD=AC+AD，等式的左右边正好是三角形ABC周长的一半，即
，有BC，AC的值，那么就能求出BD的长了，同理可求出AE的长；表示出AE•BD，即可找出与S的大小关系．
【解答】解：∵△BCD与△ACD的周长相等，BC=a，AC=b，AB=c，
∴BC+BD=AC+AD=
，
∴AD=﹣b=
，
同理CE=
，
∵∠BCA=90°，
∴a2+b2=c2，S=
ab，
可得CE•AD=×=
=
（c2﹣a2﹣b2+2ab）=
ab，
则S=CE•AD．
故选A．
【点评】此题考查了勾股定理，以及三角形面积，通过周长相等得出线段的长是解题的关键．