（本小题满分14分）
已知动圆过定点
，且与直线L:
相切，其中
.
(Ⅰ) 求动圆圆心
的轨迹方程；
（Ⅱ）设
为轨迹C上一定点，经过A作直线AB、AC分别交抛物线于B、C两点，若AB和AC的斜率之积为常数
.求证：直线BC经过一定点,并求出该定点的坐标.
（本小题满分14分）
已知动圆过定点，且与直线L:相切，其中.
(Ⅰ) 求动圆圆心的轨迹方程；
（Ⅱ）设为轨迹C上一定点，经过A作直线AB、AC分别交抛物线于B、C两点，若AB和AC的斜率之积为常数.求证：直线BC经过一定点,并求出该定点的坐标.
（本小题满分14分）
解：(Ⅰ)设
为动圆圆心，设
，
过点作直线L:
的垂线，垂足为
，
由题意知：
由抛物线的定义知，点的轨迹为抛物线，
其中
为焦点，L:为准线，
所以轨迹方程为
. ………………………………5分
(II)设
，则
，
于是
，于是
.
所以，直线BC的方程为
，
即
.
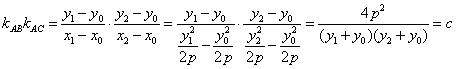
所以，
.
所以，直线BC的方程为
.
即
.
于是，直线BC经过定点
. …………………………14分