如图，已知直线y=﹣x+2与x、y轴交于M、N，若将N向右平移个单位后的N

如图，已知直线y=﹣x+2与x、y轴交于M、N，若将N向右平移个单位后的N，恰好落在反比例函数y=的图象上．

（1）求k的值；

（2）点P为双曲线上的一个动点，过点P作直线PA⊥x轴于

A点，交NM延长线于F点，过P点作PB⊥y轴于B交MN于点E．设点P的横坐标为m．

①用含有m的代数式表示点E、F的坐标

②找出图中与△EOM相似的三角形，并说明理由．

                                                 （第26题图）

解：（1）∵直线y=﹣x+2与x、y轴交于M、N，

∴M（2，0），N（0，2），

∵将N向右平移个单位后的N的坐标为（，2），

把（，2）代入y=中，

得到k=6．

（2）①∵点P的横坐标为m，

∴P（m，），

当x=m时，y=﹣m+2，

∴F（m，2﹣m），

当y=时，=﹣x+2，

∴x=2﹣，

∴E（2﹣，）．

②结论：△OME∽△FNO．

理由：如图将△ONE绕点O顺时针旋转90°得到△OMK，连接FK．

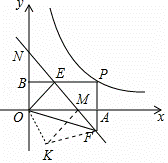
（第26题答图）

∵OM=ON，

∴∠OMN=∠ONM=∠OMK=45°，

∴∠NMK=∠FMK=90°，

∵E（2﹣，），F（m，2﹣m），

∴BE=BN=2﹣，

∴NE=MK=BE=2﹣，

∵AF=AM=m﹣2，

∴FM=AM=m﹣2，

∴FK====•（﹣2+m），

∵EF=PA=•（﹣2+m），

∴EF=FK，

∵OF=OF，OE=OK，

∴△FOE≌△FOK（SSS），

∴∠FOE=∠FOK.

∵∠EOK=90°，

∴∠EOF=45°.

∵∠OEM=∠NOE+∠ONE=∠NOE+45°，∠NOF=∠NOE+∠EOF=∠NOE+45°，

∴∠OEM=∠NOF.∵∠OME=∠ONF，

∴△OME∽△FNO．