已知抛物线y=ax2+bx+c（0＜2a＜b）的顶点为P（x0，y0），点A（1，yA）、B（0，yB）、C（－1，yC）在该抛物线上．
（Ⅰ）当a=1，b=4，c=10时，①求顶点P的坐标；②求
-的值；
（Ⅱ
）当y0≥0恒成立时，
求的最小值．
已知抛物线y=ax2+bx+c（0＜2a＜b）的顶点为P（x0，y0），点A（1，yA）、B（0，yB）、C（－1，yC）在该抛物线上．
（Ⅰ）当a=1，b=4，c=10时，①求顶点P的坐标；②求-的值；
（Ⅱ）当y0≥0恒成立时，求的最小值．
（Ⅰ）若a=1，b=4，c=10，此时抛物线的解析
式为y=x2+4x+10。
①∵y=x2+4x+10=（x+2）2+6，∴抛物线的顶点坐标为P（－2，6）。
②∵点A（1，yA）、B（0，yB）、C（－1，yC）在抛物线y=x2+4
x+10上，
∴yA=15，yB=10，yC=7。∴
。
（Ⅱ）由0＜2a＜b，得
。
由题意，如图过点A作A
A1⊥x轴于点A1，
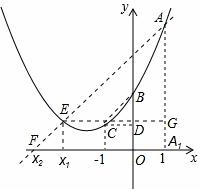
则AA1=yA，OA1=1。
过点E作EG⊥AA1于点G，易得△AEG∽△BCD。
∴
，即
。
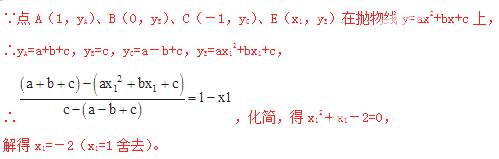
∵y0≥0恒成立，根据题意，有x2≤x1＜－1。
则1－x2≥1－x1，即1－x2≥3。
∴
的最小值为3。
【解析】（Ⅰ）将a=1，b=4，c=10代入解析式，即可得到二次函数解析式。
①将二次函数化为顶点式，即可得到得到抛物线顶点坐标。
②将A（1，yA）、B（0，yB）、C（－1，yC）分别代入解析式，即可求出yA、yB、yC的值，然后计算
的值即可。
