已知直角坐标平面内点
到点
与点
的距离之和为
．
（1）试求点
的轨迹
的方程；
（2）若斜率为
的直线
与轨迹交于
、
两点，点
为轨迹上一点，记直线
的斜率为
，直线
的斜率为
，试问：
是否为定值？请证明你的结论．
已知直角坐标平面内点到点与点的距离之和为．
（1）试求点的轨迹的方程；
（2）若斜率为的直线与轨迹交于、两点，点为轨迹上一点，记直线的斜率为，直线的斜率为，试问：是否为定值？请证明你的结论．
解：（Ⅰ） 由题知 
，
则
由椭圆的定义知点轨迹是椭圆其中
．因为
，
所以，轨迹的方程为
（2）设直线的方程为：
，
联立直线
的方程与
椭圆方程得：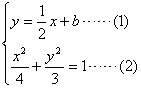
（1）代入（2）得：
化简得：
当
时，即，
也即，
时，直线与椭圆有两交点，
由韦达定理得：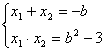
，
所以，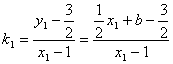
， 
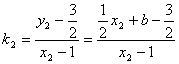
则
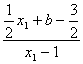
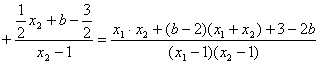
所以，
为定值。