已知函数f(x)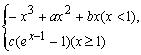＝在x＝0，x＝处存在极值。 （1）求实数a, b的值； （2）

已知函数f(x)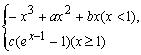＝在x＝0，x＝处存在极值。

（1）求实数a, b的值；

（2）函数y＝f(x)的图象上存在两点A, B使得△AOB是以坐标原点O为直角顶点的直角三角形，且斜边AB的中点在y轴上，求实数c的取值范围；

（3）当c＝e时，讨论关于x的方程f(x)＝kx (k∈R)的实根个数。

（1）当x＜1时，f ' (x)＝－3x²＋2ax＋b.

因为函数f(x)在x＝0, x＝处存在极值，所以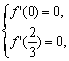

解得a＝1, b＝0.                                           …………(3分)

（2）由（1）得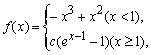

根据条件知A, B的横坐标互为相反数，不妨设A(－t, t³＋t²), B(t, f(t)(t＞0). … (4分)

若t＜1，则f(t)＝－t³＋t²,

由∠AOB是直角得·＝0，即－t²＋( t³＋t²)(－t³＋t²)＝0，

即t⁴－t²＋1＝0.此时无解；                                 …………(5分)

若t≥1，则f(t)＝c(e^t―1―1).由于AB的中点在y轴上，且∠AOB是直角，

所以B点不可能在x轴上，即t≠1.

同理·＝0，  即－t²＋( t³＋t²)·c(e^t―1―1)＝0，

整理后得  .                             …………(7分)

因为函数y＝(t＋1)(e^t-1―1)在t＞1上的值域是(0, ＋∞),

所以实数c的取值范围是(0, ＋∞).                      …………(8分)

（3）由方程f(x)＝kx,

知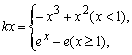

因为0一定是方程的根，                              …………(9分)

所以仅就x≠0时进行研究：

方程等价于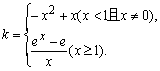

构造函数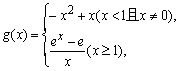                    …………(10分)

对于x＜1且x≠0部分，函数g(x)＝－x²＋x的图象是开口向下的抛物线的一部分，当x＝时取得最大值，其值域是(－∞, 0)∪(0, ]；     …………(11分)

对于x≥1部分，函数，由，

知函数g(x)在(1, ＋∞)上单调递增,则g(x)［0，+)      …………(13分)

所以, ①当k＞或k＜0时，方程f(x)＝kx有一个实根；

②当k＝或k＝0时，方程f(x)＝kx有两个实根；

③当0＜k＜时，方程f(x)＝kx有三个实根。         …………(14分)