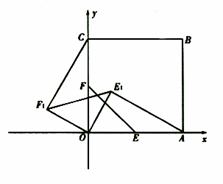
如图，已知正方形
在直角坐标系
中，点
分别在
轴、
轴的正半轴上，点
在坐标原点.等腰直角三角板
的直角顶点在原点，
分别在
上，且
将三角板绕点逆时针旋转至
的位置，连结
（1）求证：
（2）若三角板绕点逆时针旋转一周，是否存在某一位置，使得
若存在，请求出此时
点的坐标；若不存在，请说明理由.
如图，已知正方形在直角坐标系中，点分别在轴、轴的正半轴上，点在坐标原点.等腰直角三角板的直角顶点在原点，分别在上，且将三角板绕点逆时针旋转至的位置，连结
（1）求证：
（2）若三角板绕点逆时针旋转一周，是否存在某一位置，使得若存在，请求出此时点的坐标；若不存在，请说明理由.
（1）证明：∵四边形为正方形，∴
∵三角板是等腰直角三角形，∴
又三角板绕点逆时针旋转至的位置时，
∴
（2）存在.
∵
∴过点
与
平行的直线有且只有一条，并与
垂直，
又当三角板绕点逆时针旋转一周时，则点在以为圆心，以为半径的圆上，
····················· 5分
∴过点与垂直的直线必是圆的切线，又点
是圆外一点，过点与圆相切的直线有且只有2条，不妨设为
和
此时，点分别在
点和
点，满足
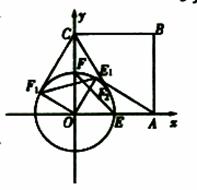
当切点
在第二象限时，点在第一象限，
在直角三角形
中，
∴
∴
∴点的横坐标为：
点的纵坐标为：
∴点的坐标为
当切点
在第一象限时，点在第四象限，
同理可求：点的坐标为
综上所述，三角板绕点逆时针旋转一周，存在两个位置，使得
此时点的坐标为
或