已知函数g（x）=ax2﹣2ax+1+b（a≠0，b＜1），在区间[2，3]上有最小值1

已知函数g（x）=ax²﹣2ax+1+b（a≠0，b＜1），在区间[2，3]上有最小值1，最大值4，设f（x）=．

（1）若不等式f（2^x）﹣k+2≥0在x∈[﹣1，1]上恒成立，求实数k的范围；

（2）方程f（|2^x﹣1|）+k（﹣3）=0有四个不同的实数解，求实数k的范围．

考点： 二次函数的性质；根的存在性及根的个数判断．

专题： 函数的性质及应用．

分析： （1）讨论a＞0和a＜0，判断g（x）在[2，3]上的单调性，根据单调性求g（x）的最值，从而求出a，b，并满足b＜1，从而求出a=1，b=0，这样可以得到不等式在x∈[﹣1，1]上恒成立，由基本不等式可求出在[﹣1，1]上的最小值2，从而k≤2；

（2）根据f（x）的解析式可将原方程变成|2^x﹣1|²﹣（2+3k）|2^x﹣1|+1+2k=0，|2^x﹣1|≠0，令|2^x﹣1|=t，得到关于t的方程：t²﹣（2+3k）t+1+2k=0，根据|2^x﹣1|=t的图象及原方程有四个不同实数解，得到方程t²﹣（2+3k）t+1+2k=0在（0，1）上有两个不同实数根，结合二次函数的图象即可得到限制k的不等式组，解不等式组即得k的范围．

解答： 解：g（x）的对称轴为x=1；

①若a＞0，则g（x）在[2，3]上单调递增；

∴g（x）在[2，3]上的最小值为g（2）=1+b=1，最大值为g（3）=3a+1+b=4；

∴a=1，b=0；

②若a＜0，g（x）在[2，3]上单调递减；

∴g（x）在[2，3]上的最小值为g（3）=3a+1+b=1，最大值为g（2）=1+b=4；

∴a=﹣1，b=3；

∵b＜1；

∴a=1，b=0；

∴g（x）=x²﹣2x+1；

∴；

∴不等式f（2^x）﹣k+2≥0在[﹣1，1]上恒成立，化成在x∈[﹣1，1]上恒成立；

∵，当x=0时取“=”；

∴在[﹣1，1]上的最小值为2；

∴k≤2；

∴实数k的范围为（﹣∞，2]；

（2）方程化为；

即|2^x﹣1|²﹣（2+3k）|2^x﹣1|+1+2k=0，2^x﹣1≠0；

令|2^x﹣1|=t，则方程化为t²﹣（2+3k）t+（1+2k）=0，（t≠0）；

可画出t=|2^x﹣1|的图象如下所示：

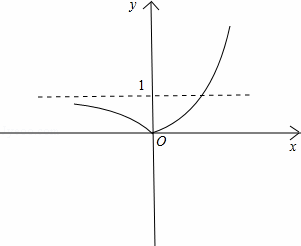
∵原方程有四个不同的解；

∴方程t²﹣（2+3k）t+1+2k=0有两个不同实数根，且都在区间（0，1）上；

设h（t）=t²﹣（2+3k）t+1+2k，则k需满足：

；

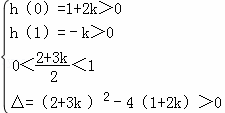解得；

∴实数k的范围为（）．

点评： 考查二次函数的单调性，根据单调性求函数在闭区间上的最值，以及运用基本不等式求函数最值，能够画出函数|2^x﹣1|的图象，熟悉并会运用二次函数图象．