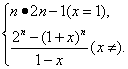,公比q是
的展开式中的第二项（按x的降幂排列）. （1）用n,x表示通项an与前n项和Sn;
(2)若
，用n,x表示An.
,公比q是的展开式中的第二项（按x的降幂排列）. （1）用n,x表示通项an与前n项和Sn;
(2)若，用n,x表示An.
·A
,∴
即
∴m=3.
由（x+
)4知T2=C
·x4-1·(
)=x.
∴an=xn-1,Sn=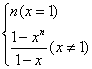
.
(2)当x=1时，Sn=n,
An=C
+2C
+3C
+…+nC
.
又∵An=nC
+(n-1)C
+(n-2)C
+…+C
+0·C
,
∴2An=n(C
+C
+C
+…+C
).
∴An=n·2n-1.
当x≠1时，Sn=
,
An=
=
［（C
+C
+C
+…+C
)-(xC
+x2C
+x3C
+…+xnC
)］
=
［2n-1-(1+xC
+x2C
+…+xnC
-1)］
=
［2n-(1+x)n］.
∴An=