（本题满分
分）若
是函数
的两个极值点．
（Ⅰ）若
，求函数
的解析式；
（Ⅱ）若
，求
的最大值；
（Ⅲ）若
为函数
的一个极值点，设函数
，当
时求
的最大值．
（本题满分分）若是函数的两个极值点．
（Ⅰ）若，求函数的解析式；
（Ⅱ）若，求的最大值；
（Ⅲ）若为函数的一个极值点，设函数，当时求的最大值．
解：（Ⅰ）∵，∴
依题意有和1是方程
的两根
∴
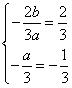解得
，∴
．（经检验，适合）．……4分
（Ⅱ）∵,
依题意，
是方程
的两个根，∵
且，
∴
．∴
∵
∴
．
设
，则
．
由
得
，由
得
．
即函数
在区间
上是增函数，在区间
上是减函数，
∴当
时，有极大值为324，∴在
上的最大值是324，
∴的最大值为18． ……………………………9分
（Ⅲ）∵是的一个极值点，
∴
，又
即
，
∵
，
∴
，则
，
即
，
∴当
时，
有最大值
．………………15分