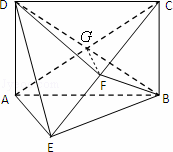
如图所示的几何体中,四边形ABCD为矩形,AD⊥平面,AE=EB=BC=2,F为CE上的点,且BF⊥平面ACE.
(1)求证:AE∥平面BFD;
(2)求三棱锥C﹣BGF的体积.
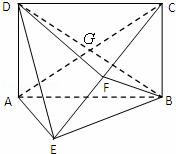
如图所示的几何体中,四边形ABCD为矩形,AD⊥平面,AE=EB=BC=2,F为CE上的点,且BF⊥平面ACE.
(1)求证:AE∥平面BFD;
(2)求三棱锥C﹣BGF的体积.

解答: (1)证明:如图,
由题意可得G是AC的中点,连接FG,
∵BF⊥平面ACE,则CE⊥BF,而BC=BE,
∴F是EC中点,
在△AEC中,FG∥AE,∴AE∥平面BFD;
(2)解:∵AE∥平面BFD,∴AE∥FG,
由题可得AE⊥平面BCE,∴FG⊥平面BCE.
∵G是AC的中点,F是CE中点,∴AE∥FG且FG=![]() ,
,
∵BF⊥平面ACE,∴BF⊥CE,∴Rt△BCE中,BF=![]() ,
,
∴![]() ,
,
∴![]() =
=![]() .
.