某饮料经营部每天的固定成本为50元，其销售的每瓶饮料进价为5元．

某饮料经营部每天的固定成本为50元，其销售的每瓶饮料进价为5元．设销售单价为x元时，日均销售量为y瓶，x与y的关系如下：

（1）求y与x的函数关系式并直接写出自变量x的取值范围；

（2）每瓶饮料的单价定为多少元时，日均毛利润最大？最大利润是多少？

（毛利润=售价﹣进价﹣固定成本）

（3）每瓶饮料的单价定为多少元时，日均毛利润为430元？根据此结论请你直接写出销售单价在什么范围内时，日均毛利润不低于430元．

【考点】二次函数的应用．

【分析】（1）设y与x的函数关系式为y=kx+b，然后把x=6，y=270；x=7，y=240代入求出k、b的值；根据y大于等于0求x的取值范围；

（2）根据毛利润=售价﹣进价﹣固定成本列出函数关系，然后整理成顶点式，再根据二次函数的最值问题解答；

（3）把y=430元代入函数关系式，解关于x的一元二次方程即可；根据二次函数图象的增减性求出范围．

【解答】解：（1）设y与x的函数关系式为y=kx+b，

把x=6，y=270；x=7，y=240分别代入，

得，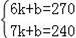

解得，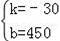

∴y=﹣30x+450，

y=﹣30x+450＞0，

解得x＜15，

∴取值范围是5＜x＜15；

（2）根据题意得，毛利润S=x（﹣30x+450）﹣5（﹣30x+450）﹣50

=﹣30x²+600x﹣2300

=﹣30（x﹣10）²+700，

∴当单价定为10元时，日均毛利润最大，最大利润是700元；

（3）根据题意，S=﹣30x²+600x﹣2300=430，

整理得x²﹣20x+91=0，

即（x﹣7）（x﹣13）=0，

∴x﹣7=0或x﹣13=0，

解得x₁=7，x₂=13，

∴每瓶饮料的单价定为7元或13元时，日均毛利润为430元，

∵﹣30＜0，

∴销售单价：7≤x≤13时，日均毛利润不低于430元．