如图，牧童在A处放牛，其家在B处，A，B到河岸CD的距离分别为AC，BD，且AC＝BD，若A到河岸CD的中点的距离为500 m.
(1)牧童从A处把牛牵到河边饮水后再回家，试问在何处饮水，所走路程最短？在图中作出
该处，并说明理由；
(2)最短
路程是多少？
如图，牧童在A处放牛，其家在B处，A，B到河岸CD的距离分别为AC，BD，且AC＝BD，若A到河岸CD的中点的距离为500 m.
(1)牧童从A处把牛牵到河边饮水后再回家，试问在何处饮水，所走路程最短？在图中作出该处，并说明理由；
(2)最短路程是多少？
解：(1)作法：如图作点A关于CD的对称点A′；
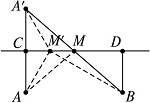
连接A′B
交CD于点M.则点M即为所求的点．
证明：在CD上任取一点M′，连接AM′，A′
M′，BM′，AM，
因为直线CD是A，A′的对称轴，M，M′在CD上，
所以AM＝A′M，AM′＝A′M′，所以AM＋BM＝A′M＋BM＝A′B，
在△A′M′B
中，因为A′M′＋BM′＞A′B，
所以AM′＋BM′＝A′M′＋BM′＞AM＋BM，即AM＋BM最小．
(2)由(1)可得AM＝A′M，A′C＝AC＝BD，所以△A′CM≌△BDM，
即A′M＝BM，CM＝DM，所以M为CD的中点，且A′B＝2AM，
因为AM＝500 m，所以A′B＝AM＋BM＝2AM＝1 000 m．即最短路程为1 000 m.