如图,OABC是一张放在平面直角坐标系中的矩形纸片,O为坐标原点,点A在

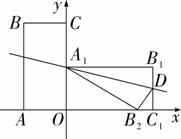
如图,OABC是一张放在平面直角坐标系中的矩形纸片,O为坐标原点,点A在x轴上,点C在y轴上,OA=9,OC=15,将矩形纸片OABC绕O点顺时针旋转90°得到矩形OA₁B₁C₁.将矩形OA₁B₁C₁折叠,使得点B₁落在x轴上,并与x轴上的点B₂重合,折痕为A₁D.
(Ⅰ)求点B₂的坐标;
(Ⅱ)求折痕A₁D所在直线的解析式;
(Ⅲ)在x轴上是否存在点P,使得∠BPB₁为直角？若存在,求出点P的坐标;若不存在,请说明理由.

解:(Ⅰ)由条件知,B₂A₁=B₁A₁=BA=15,A₁O=B₁C₁=BC=9,
∴在Rt△A₁OB₂中,OB₂＝＝12,
∴点B₂坐标为(12,0);
(Ⅱ)B₂C₁=15－12=3,DC₁=m,则B₁D=9－m,
∵B₁D=B₂D,
∴＝9−m,
解得m=4,
∴D点的坐标为(15,4),
又∵A₁(0,9),
设折痕A₁D所在直线的解析式为y=kx＋b(k≠0),
∴,
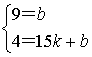解得,
即折痕A₁D所在直线的解析式为y＝−x＋9;
(Ⅲ)假设存在P点,
∵∠BPA＋∠BPB₁＋∠B₁PC₁=180°,∠BPB₁=90°,
∴∠BPA＋∠B₁PC₁=90°,
∵∠BAP=90°,∠ABP＋∠BPA=90°,
∴∠ABP=∠B₁PC₁.
在△BAP和△PC₁B₁中,,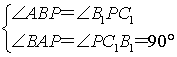
∴△BAP∽△PC₁B₁.
∴,
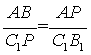∵AB=15,C₁B₁=9,AC₁=24,设PC₁的长为m,
∴,
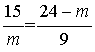解得m₁=15或m₂=9.
经检验m₁=15或m₂=9是方程的两根,
当PC₁=15时,P点坐标为(0,0);
当PC₁=9时,P点坐标为(6,0).
综上所述,P点坐标为(0,0),(6,0).