如图，△AOB中，∠AOB＝90°，AO＝3，BO＝6，△AOB绕顶点O逆时针旋转到△A′OB′处，此时线段A′B′与BO的交点E为BO的中点，则线段B′E的长度为 ．
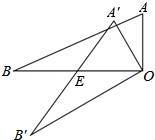
如图，△AOB中，∠AOB＝90°，AO＝3，BO＝6，△AOB绕顶点O逆时针旋转到△A′OB′处，此时线段A′B′与BO的交点E为BO的中点，则线段B′E的长度为 ．
．
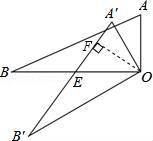
【分析】利用勾股定理列式求出AB，根据旋转的性质可得AO＝A′O，A′B′＝AB，再求出OE，从而得到OE＝A′O，过点O作OF⊥A′B′于F，利用三角形的面积求出OF，利用勾股定理列式求出EF，再根据等腰三角形三线合一的性质可得A′E＝2EF，然后根据B′E＝A′B′﹣A′E代入数据计算即可得解．
【解答】解：∵∠AOB＝90°，AO＝3，BO＝6，
∴AB＝
＝
＝3
，
∵△AOB绕顶点O逆时针旋转到△A′OB′处，
∴AO＝A′O＝3，A′B′＝AB＝3
，
∵点E为BO的中点，
∴OE＝
BO＝×6＝3，
∴OE＝A′O，
过点O作OF⊥A′B′于F，
S△A′OB′＝×3•OF＝
×3×6，
解得OF＝
，
在Rt△EOF中，EF＝
＝
＝
，
∵OE＝A′O，OF⊥A′B′，
∴A′E＝2EF＝2×＝
（等腰三角形三线合一），
∴B′E＝A′B′﹣A′E＝3
﹣＝
．
故答案为：
．
【点评】本题考查了旋转的性质，勾股定理的应用，等腰三角形三线合一的性质，以及三角形面积，熟练掌握旋转变换只改变图形的位置不改变图形的形状与大小是解题的关键．