如图,已知椭圆
+
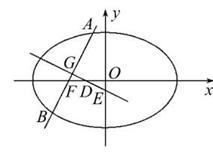
=1的左焦点为F,过点F的直线交椭圆于A,B两点,线段AB的中点为G,AB的中垂线与x轴和y轴分别交于D,E两点.
(1)若点G的横坐标为-
,求直线AB的斜率.
(2)记△GFD的面积为S1,△OED(O为原点)的面积为S2.试问:是否存在直线AB,使得S1=S2?说明理由.
如图,已知椭圆+=1的左焦点为F,过点F的直线交椭圆于A,B两点,线段AB的中点为G,AB的中垂线与x轴和y轴分别交于D,E两点.
(1)若点G的横坐标为-,求直线AB的斜率.
(2)记△GFD的面积为S1,△OED(O为原点)的面积为S2.试问:是否存在直线AB,使得S1=S2?说明理由.
【解析】(1)依题意,直线AB的斜率存在,
设其方程为y=k(x+1),
将其代入+=1,
整理得(4k2+3)x2+8k2x+4k2-12=0,
设A(x1,y1),B(x2,y2),所以x1+x2=
,
故点G的横坐标为
=
.
依题意,得=-,解得k=±
.
(2)假设存在直线AB,使得S1=S2,显然直线AB不能与x,y轴垂直.
由(1)可得G
,
因为DG⊥AB,所以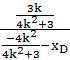
×k=-1,
解得xD=
,即D
,
因为△G
FD∽△OED,
所以S1=
S2⇔|GD|=|OD|,
所以
=
,
整理得8k2+9=0,因为此方程无解,
所以不存在直线AB,使得S1=S2.