(1)将十字形的面积表示为θ的函数;
(2)θ为何值时,十字形的面积最大?最大面积是多少?
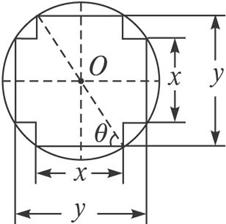
图3-1
(1)将十字形的面积表示为θ的函数;
(2)θ为何值时,十字形的面积最大?最大面积是多少?
图3-1
解
:(1)设S为十字形的面积,则S=2xy-x2=2sinθcosθ-cos2θ(
＜θ＜
).
(2)解法一:S=2sinθcosθ-cos2θ
=sin2θ-
cos2θ-
=
sin(2θ-φ)-
,
其中φ=arccos
,
当sin(2θ-φ)=1,即2θ-φ=
时,S最大.
所以,当θ=
+
arccos
时,S最大.
S的最大值为
.
解法二:因为S=2sinθcosθ-cos2θ,
所以S′=2cos2θ-2sin2θ+2sinθcosθ=2cos2θ+sin2θ.
令S′=0,即2cos2θ+sin2θ=0,
可解得θ=
+
arctan(-2).
所以,当θ=
+
arctan(-2)时,S最大,S的最大值为
.