已知集合A={x|x2-4x-5≥0},集合B={x|2a≤x≤a+2}.
(1)若a=-1,求A∩B和A∪B;
(2)若A∩B=B,求实数a的取值范围.
已知集合A={x|x2-4x-5≥0},集合B={x|2a≤x≤a+2}.
(1)若a=-1,求A∩B和A∪B;
(2)若A∩B=B,求实数a的取值范围.
解 (1)A={x|x≤-1或x≥5},B={x|-2≤x≤1},所以A∩B={x|-2≤x≤-1},
A∪B={x|x≤1或x≥5}.
(2)因为A∩B=B,所以B⊆A.
①若B=∅,则2a>a+2,得a>2;
②若B≠∅,则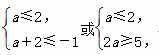
所以a≤-3.
综上知,实数a的取值范围是{a|a>2或a≤-3}.