已知函数![]() 令
令![]() .
.
(Ⅰ)当![]() 时,求函数
时,求函数![]() 的单调递增区间;
的单调递增区间;
(Ⅱ)若关于![]() 的不等式
的不等式![]() 恒成立,求整数
恒成立,求整数![]() 的最小值;
的最小值;
(Ⅲ)若![]() ,正实数
,正实数![]() 满足
满足![]() ,证明:
,证明:![]() .
.
已知函数![]() 令
令![]() .
.
(Ⅰ)当![]() 时,求函数
时,求函数![]() 的单调递增区间;
的单调递增区间;
(Ⅱ)若关于![]() 的不等式
的不等式![]() 恒成立,求整数
恒成立,求整数![]() 的最小值;
的最小值;
(Ⅲ)若![]() ,正实数
,正实数![]() 满足
满足![]() ,证明:
,证明:![]() .
.
(Ⅰ)![]()
![]()
由![]() 得
得![]() 又
又![]() 所以
所以![]() .所以
.所以![]() 的单增区间为
的单增区间为![]() .
.
(Ⅱ)方法一:令![]()
所以![]() .
.
当![]() 时,因为
时,因为![]() ,所以
,所以![]() ,所以
,所以![]() 在
在![]() 上是递增函数,
上是递增函数,
又因为![]() 所以关于
所以关于![]() 的不等式
的不等式![]() 不能恒成立.
不能恒成立.
当![]() 时,
时,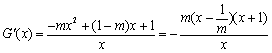 .
.
令![]() 得
得![]() ,所以当
,所以当![]() 时,
时,![]() ;当
;当![]() 时,
时,![]() .
.
因此函数![]() 在
在![]() 是增函数,在
是增函数,在![]() 是减函数.
是减函数. ![]()
故函数![]() 的最大值为
的最大值为![]() …………8分
…………8分
令![]() 因为
因为![]()
又因为![]() 在
在![]() 上是减函数,所以当
上是减函数,所以当![]() 时,
时,![]() .
.
所以整数![]() 的最小值为. ……………10分
的最小值为. ……………10分
方法二:(2)由![]() 恒成立,得
恒成立,得![]() 在
在![]() 上恒成立.
上恒成立.
问题等价于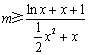 在
在![]() 上恒成立.
上恒成立.
令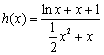 ,只要
,只要![]() . ……………………6分
. ……………………6分
因为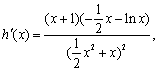 令
令![]() 得
得![]() .
.
设![]() ,因为
,因为![]() ,所以
,所以![]() 在
在![]() 上单调递减,
上单调递减,
不妨设![]() 的根为
的根为![]() .当
.当![]() 时,
时,![]() 当
当![]() 时,
时,![]() .
.
所以![]() 在
在![]() 上是增函数;在
上是增函数;在![]() 上是减函数.
上是减函数.
所以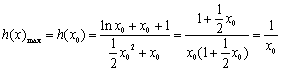 .
.
因为![]()
![]()
所以![]() 此时
此时![]() 所以
所以![]() 即整数
即整数![]() 的最小值为2
的最小值为2
(Ⅲ)当![]() 时,
时,![]()
由![]() 即
即![]()
从而![]()
令![]() 则由
则由![]() 得,
得,![]()
可知![]() 在区间(0,1)上单调递减,在区间
在区间(0,1)上单调递减,在区间![]() 上单调递增。所以
上单调递增。所以![]()
所以![]() 即
即![]() 成立.
成立.