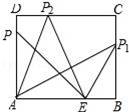
如图是一张长方形纸片ABCD，已知AB=8，AD=7，E为AB上的一点，AE=5，点P在长方形ABCD的一边上，要使△AEP是等腰三角形，则△AEP的底边长为 ．
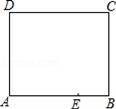
如图是一张长方形纸片ABCD，已知AB=8，AD=7，E为AB上的一点，AE=5，点P在长方形ABCD的一边上，要使△AEP是等腰三角形，则△AEP的底边长为 ．
5或5
或4
．
【考点】LB：矩形的性质；KI：等腰三角形的判定．
【分析】分情况讨论：①当AP=AE=5时，则△AEP是等腰直角三角形，得出底边PE=
AE=5即可；
②当PE=AE=5时，求出BE，由勾股定理求出PB，再由勾股定理求出等边AP即可；
③当PA=PE时，底边AE=5；即可得出结论．
【解答】解：如图所示：
①当AP=AE=5时，
∵∠BAD=90°，
∴△AEP是等腰直角三角形，
∴底边PE=
AE=5；
②当PE=AE=5时，
∵BE=AB﹣AE=8﹣5=3，∠B=90°，
∴PB=
=4，
∴底边AP=
=
=4
；
③当PA=PE时，底边AE=5；
综上所述：等腰三角形AEP的对边长为5
或4或5；
故答案为：5或5
或4
