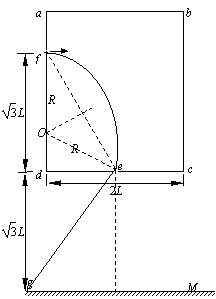
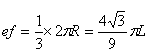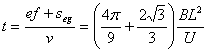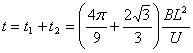如图所示，abcd是一个长方形盒子，在ad边和cd边上各开有小孔f和e，e是cd边上的中点，荧光屏M平行cd放置，能显示从e孔射出的粒子落点位置。盒子内有一方向垂直于abcd平面的匀强磁场，磁感应强度大小为B。粒子源不断地发射相同的带电粒子，粒子的初速度可以忽略。粒子经电压为U的电场加速后，从f孔垂直于ad边射入盒内，再经磁场偏转后恰好从e孔射出。若已知fd＝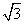
L，cd＝2L，屏M与cd间的距离为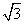L，不计粒子重力和粒子之间的相互作用力。
（1）求带电粒子的比荷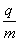
；
（2）求带电粒子从f孔运动到屏M的时间t；
（3）若撤去磁场，盒子内加一平行于ad边的匀强电场，粒子经电场偏转后仍恰好从e孔射出，求电场强度大小。
（1）带电粒子在电场中加速．根据动能定理得
qU＝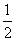
mv2，解得v＝
（1分）
粒子进入磁场后做匀速圆周运动，轨迹如图所示，设圆周半径为R，在三角形Ode中，有
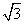(L－R)2＋L2＝R2
解得R＝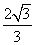
L
（1分）
又qvB＝m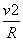
（1分）
解得＝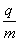
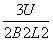. （1分）
（2）粒子运动轨迹如图所示
在三角形Ode中，∠dOe＝arcsin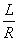
＝60°
则弧所对应的圆心角是120°
得弧长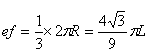
（1分）
粒子出磁场后，轨迹为eg 长度seg=2L （1分）
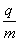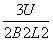＝代入v＝得：v＝
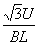（1分）
运动总时间
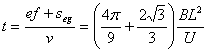（1分）
（3）换电场后，粒子做类平抛运动
入射方向匀速运动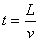 
（1分）
ad方向匀加速运动 
（1分）
电场中的加速度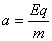
由上述三式整理得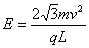
（1分）
将qU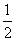＝mv2代入得
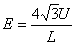（1分）
（说明：解法二评分标准
粒子在磁场中做匀速圆周运动
其周期T＝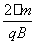
代入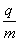得：T＝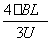
在三角形Ode中，∠dOe＝arcsin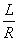＝60°，则弧所对应的圆心角是120°
所以磁场中的运动时间
t1＝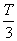
＝
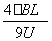（1分）
粒子出磁场后，做匀速直线运动，轨迹为eg
由几何知识得 seg=2L （1分）
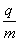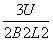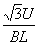＝代入v＝得：v＝ （1分）
所以磁场外的运动时间t2＝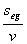
＝
运动总时间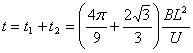
（1分）
