如图，□A
BCD中，BD是它的一条对角线，过A、C两点作AE⊥BD，CF⊥BD，垂足分别为E、F，延长AE、CF分别交CD、AB于M、N。
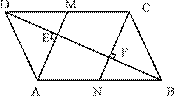（1）（4分）求证：四边形CMAN是平行四边形。
（2）（4分）已知DE＝4，FN＝3，求BN的长。
如图，□ABCD中，BD是它的一条对角线，过A、C两点作AE⊥BD，CF⊥BD，垂足分别为E、F，延长AE、CF分别交CD、AB于M、N。
（1）（4分）求证：四边形CMAN是平行四边形。
（2）（4分）已知DE＝4，FN＝3，求BN的长。
【考点】平行四边形的判定与性质，全等三角形的判定与性质，勾股定理．
【分析】（1）通过AE⊥BD，CF⊥BD证明AE∥CF，再由四边形ABCD是平行四边形得到AB∥CD，由两组对边分别平行的四边形是平行四边形可证得四边形CMAN是平行四边形；
（2）先证明两三角形全等得DE=BF=4，再由勾股定理得BN=5．
【解答】⑴证明：∵AE⊥BD CF⊥BD
∴AE∥CF
又∵四边形ABCD是平行四边形
∴AB∥CD
∴四边形CMAN是平行四边形 （4分）
⑵由⑴知四边形CMAN是平行四边形
∴CM=AN.
又∵四边形ABCD是平行四边形
∴ AB=CD，∠MDE=∠NBF.
∴AB-AN=CD-CM，即DM=BN.
在△MDE和∠NBF中
∠MDE=∠NBF
∠DEM=∠BFN=90°
DM=BN
∴△MDE≌∠NBF
∴DE=BF=4，（2分）
由勾股定理得BN=
=
=5（4分）.
答：BN的长为5.
【点评】本题主要考查了平行四边形的判定及其性质，全等三角形的判定与性质，勾股定理；灵活运用判定、性质及定理来分析、判断、推理或解答是解题的关键．