设异面直线![]() 、
、![]() 成
成![]() 角,它们的公垂线段为
角,它们的公垂线段为![]() 且
且![]() ,线段AB的长为4,两端点A、B分别在
,线段AB的长为4,两端点A、B分别在![]() 、
、![]() 上移动,则AB中点P的轨迹是 。
上移动,则AB中点P的轨迹是 。
设异面直线![]() 、
、![]() 成
成![]() 角,它们的公垂线段为
角,它们的公垂线段为![]() 且
且![]() ,线段AB的长为4,两端点A、B分别在
,线段AB的长为4,两端点A、B分别在![]() 、
、![]() 上移动,则AB中点P的轨迹是 。
上移动,则AB中点P的轨迹是 。
![]()
AB的中点P过EF的中点O且与![]() 、
、![]() 平行的平面
平行的平面![]() 内,于是空间的问题转化为平面问题。取EF的中点O,过O作
内,于是空间的问题转化为平面问题。取EF的中点O,过O作![]()
则 ![]() 、
、![]() 确定平面
确定平面![]() ,
,![]()
且A在![]() 内的射影必在
内的射影必在![]() 上,B在
上,B在![]() 内的射影必在
内的射影必在![]() 上,AB的中点P必在
上,AB的中点P必在![]() H ,如图1所示。
H ,如图1所示。
又 ![]()
易得 ![]() ,
,
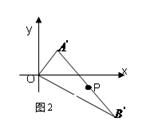
现求线段![]() 在移动时,其中点P的轨迹。以
在移动时,其中点P的轨迹。以![]() 的平分线为
的平分线为![]() 轴,O为原点,建立直角坐标系,如图2所示。不妨设
轴,O为原点,建立直角坐标系,如图2所示。不妨设![]() 。在
。在![]() 中,
中,![]() ①。设
①。设![]() 的中点P的坐标为
的中点P的坐标为![]() ,则
,则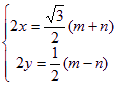 ,即
,即 ,代入①消去
,代入①消去![]() 、
、![]() ,得
,得![]() ,于是得到的是椭圆②夹在
,于是得到的是椭圆②夹在![]() 内的弧,在另外的情形中,同样得到椭圆②的其余弧,故点P的轨迹是EF的中垂面上以O为中心的椭圆
内的弧,在另外的情形中,同样得到椭圆②的其余弧,故点P的轨迹是EF的中垂面上以O为中心的椭圆![]() 。
。