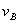
、
,第1个小物块与车槽碰撞后的共同速度为
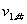
，由动量守恒定律和能量守恒定律得：mBvB=mCvC EP =
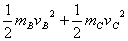
解得：
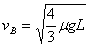
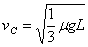
由上可知，物体B先与车槽A相撞，有：mBvB =（mA+mB）v1共 解得：v1共=
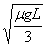
(2)设物体B经时间
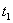
与车槽A相撞，车槽A与B球相撞后经时间
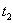
速度减为0, 物体B与车槽A相撞的时间：t1=
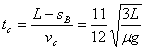
车槽A与B物体相撞后，一起向左匀减速运动，由牛顿第二定律有：
即 
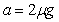
车槽A和物体B相撞后速度减为0的时间：
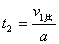
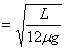
车槽向左移动的距离为：
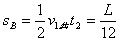
在（t1+t2）这段时间内，物体C移动的距离为：
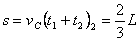
由上解得：即s＜L-
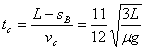
, 这说明在C 与A相撞前A已停止运动,所以，第2个小物块C经与车槽相碰撞的时间为： （3）设第2个小物块与车槽碰撞后的共同速度
，车槽向右运动的距离为
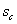
,物体 C和车槽相撞，有：mCvC=（mA+mB+mC）v2共 即 v2共=
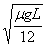
对车槽系统，由动能定理得：
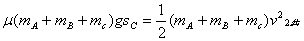
即 
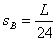
整个运动过程中，车槽向右运动的位移大小为：
=
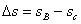
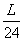
， 方向向左