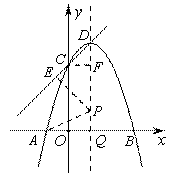
如图10，抛物线y＝－x2＋bx＋c与x轴分别交于点A、B，与y轴交于点C，

如图10，抛物线y＝－x²＋bx＋c与x轴分别交于点A、B，与y轴交于点C，且OA＝1，OB＝3，顶点为D，对称轴交x轴于点Q．

（1）求抛物线对应的二次函数的表达式；

（2）点P是抛物线的对称轴上一点，以点P为圆心的圆经过A、B两点，且与直线CD相切，求点P的坐标；

（3）在抛物线的对称轴上是否存在一点M，使得△DCM∽△BQC？如果存在，求出点M的坐标；如果不存在，请说明理由．

解：（1）∵OA＝1，OB＝3，

∴A（－1,0），B（3,0）．……………………………………1分

代入y＝－x²＋bx＋c，得

．………………………2分

解得　b＝2，c＝3．

∴抛物线对应二次函数的表达式为：y＝－x²＋2x＋3；……3分

（2）如图，设直线CD切⊙P于点E．连结PE、PA，作CF⊥DQ于点F．

∴PE⊥CD，PE＝PA．　……………………………4分

由y＝－x²＋2x＋3，得

对称轴为直线x＝1，C（0，3）、D（1，4）．……5分

∴DF＝4－3＝1，CF＝1，

∴DF＝CF，

∴△DCF为等腰直角三角形．

∴∠CDF＝45°，

∴∠EDP＝∠EPD＝45°，

∴DE＝EP，

∴△DEP为等腰三角形．　

设P（1，m），

∴EP²＝（4－m）²．　………………………6分

在△APQ中，∠PQA＝90°，

∴AP²＝AQ²＋PQ²＝[1－（－1）]²＋m²．……7分

∴　　　（4－m）²＝[1－（－1）]²＋m²．

解得，　　　　　　m＝．

∴点P的坐标为（1，）或（1，）．………8分

（3）存在点M，使得△DCM∽△BQC．……………9分

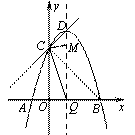如图，连结CQ、CB、CM，

∵C（0，3），OB＝3，∠COB＝90°，

∴△COB为等腰直角三角形，

∴∠CBQ＝45°，BC＝3．

由（2）可知，∠CDM＝45°，CD＝，

∴∠CBQ＝∠CDM．……………………………10分

∴△DCM∽△BQC分两种情况．

当时，

∴，解得　DM＝．

∴QM＝DQ－DM＝4－＝．

∴M₁（1，）．…………………………………11分

当时，

∴，解得　DM＝3．

∴QM＝DQ－DM＝4－3＝1．

∴M₂（1，1）．

综上，点M的坐标为（1，）或（1，1）．