小磊要制作一个三角形的钢架模型，在这个三角形中，长度为x（单位：cm）的边与这条边上的高之和为40cm，这个三角形的面积S（单位：cm2）随x（单位：cm）的变化而变化．
（1）请直接写出S与x之间的函数关系式（不要求写出自变量x的取值范围）；
（2）当x是多少时，这个三角形面积S最大？最大面积是多少？
小磊要制作一个三角形的钢架模型，在这个三角形中，长度为x（单位：cm）的边与这条边上的高之和为40cm，这个三角形的面积S（单位：cm2）随x（单位：cm）的变化而变化．
（1）请直接写出S与x之间的函数关系式（不要求写出自变量x的取值范围）；
（2）当x是多少时，这个三角形面积S最大？最大面积是多少？
【考点】二次函数的应用．
【分析】（1）S=
x×这边上的高，把相关数值代入化简即可；
（2）结合（1）得到的关系式，利用公式法求得二次函数的最值即可．
【解答】解：（1）S=﹣x2+20x；
（2）∵﹣＜0，
∴S有最大值，
∴当x=﹣
=﹣
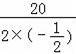
=20时，
S有最大值为
=
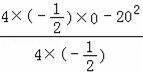
=200cm2．
∴当x为20cm时，三角形最大面积是200cm2．
【点评】考查二次函数的应用；掌握二次函数的顶点为（﹣
，），是解决本题的关键．