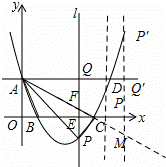
如图，在平面直角坐标系中，抛物线y=mx2﹣8mx+4m+2（m＞2）与y轴的交点为A，与x轴的交点分别为B（x1，0），C（x2，0），且x2﹣x1=4，直线AD∥x轴，在x轴上有一动点E（t，0）过点E作平行于y轴的直线l与抛物线、直线AD的交点分别为P、Q．
（1）求抛物线的解析式；
（2）当0＜t≤8时，求△APC面积的最大值；
（3）当t＞2时，是否存在点P，使以A、P、Q为顶点的三角形与△AOB相似？若存在，直接写出t的值；若不存在，请说明理由．
如图，在平面直角坐标系中，抛物线y=mx2﹣8mx+4m+2（m＞2）与y轴的交点为A，与x轴的交点分别为B（x1，0），C（x2，0），且x2﹣x1=4，直线AD∥x轴，在x轴上有一动点E（t，0）过点E作平行于y轴的直线l与抛物线、直线AD的交点分别为P、Q．
（1）求抛物线的解析式；
（2）当0＜t≤8时，求△APC面积的最大值；
（3）当t＞2时，是否存在点P，使以A、P、Q为顶点的三角形与△AOB相似？若存在，直接写出t的值；若不存在，请说明理由．
）
解：（1）由题意知x1、x2是方程mx2﹣8mx+4m+2=0的两根，
∴x1+x2=8， 由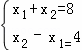
解得：
∴B（2，0）、C（6，0） 则4m﹣16m+4m+2=0， 解得：m=
，
∴该抛物线解析式为：y=
；…………（2分）
（2）可求得A（0，3） 设直线AC的解析式为：y=kx+b，
∵
∴
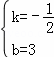∴直线AC的解析式为：y=﹣
x+3，
要构成△APC，显然t≠6，分两种情况讨论：
①当0＜t＜6时，设直线l与AC交点为F，则：F（t，﹣
），
∵P（t，
），∴PF=
，
∴S△APC=S△APF+S△CPF
=
=
=
， 此时最大值为：
，…………（5分）
②当6≤t≤8时，设直线l与AC交点为M，则：M（t，﹣
），
∵P（t，
），∴PM=
，
∴S△APC=S△APF﹣S△CPF=
=
=
， 当t=8时，取最大值，最大值为：12，
综上可知，当0＜t≤8时，△APC面积的最大值为12；…………（8分）
（3）
∴t=
或t=
或t=14．…………（11分）
