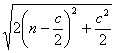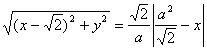е·ІзҹҘ![]() =(cпјҢo)(c>o)пјҢ
=(cпјҢo)(c>o)пјҢ![]() =(
=(![]() пјҢ
пјҢ![]() )(
)(![]() R)пјҢ
R)пјҢ![]() зҡ„жңҖе°ҸеҖјдёә1пјҢиӢҘеҠЁзӮ№PеҗҢж—¶ж»Ўи¶ідёӢеҲ—дёүдёӘжқЎд»¶пјҡв‘
зҡ„жңҖе°ҸеҖјдёә1пјҢиӢҘеҠЁзӮ№PеҗҢж—¶ж»Ўи¶ідёӢеҲ—дёүдёӘжқЎд»¶пјҡв‘ ![]() пјӣв‘Ў
пјӣв‘Ў![]() пјҢе…¶дёӯ
пјҢе…¶дёӯ![]() Rпјӣв‘ўеҠЁзӮ№Pзҡ„иҪЁиҝ№Cз»ҸиҝҮзӮ№B(0пјҢдёҖ1)пјҺ
Rпјӣв‘ўеҠЁзӮ№Pзҡ„иҪЁиҝ№Cз»ҸиҝҮзӮ№B(0пјҢдёҖ1)пјҺ
(1)жұӮ![]() зҡ„еҖјпјӣ
зҡ„еҖјпјӣ
(2)жұӮжӣІзәҝCзҡ„ж–№зЁӢпјӣ
(3)жҳҜеҗҰеӯҳеңЁж–№еҗ‘еҗ‘йҮҸдёә![]() вү 0)зҡ„зӣҙзәҝ
вү 0)зҡ„зӣҙзәҝ![]() пјҢдҪҝ
пјҢдҪҝ![]() дёҺжӣІзәҝCдәӨдәҺдёӨдёӘдёҚеҗҢзҡ„зӮ№MгҖҒNпјҢдё”
дёҺжӣІзәҝCдәӨдәҺдёӨдёӘдёҚеҗҢзҡ„зӮ№MгҖҒNпјҢдё”![]() ?иӢҘеӯҳеңЁпјҢжұӮеҮәkзҡ„еҸ–еҖјиҢғеӣҙпјӣиӢҘдёҚеӯҳеңЁпјҢиҜ·иҜҙжҳҺзҗҶз”ұпјҺ
?иӢҘеӯҳеңЁпјҢжұӮеҮәkзҡ„еҸ–еҖјиҢғеӣҙпјӣиӢҘдёҚеӯҳеңЁпјҢиҜ·иҜҙжҳҺзҗҶз”ұпјҺ