（06年四川卷理）（12分）
已知两定点
满足条件
的点P的轨迹是曲线E，直线ｙ＝kx－1与曲线E交于A、B两点。如果
且曲线E上存在点C，使
求
。
（06年四川卷理）（12分）
已知两定点满足条件的点P的轨迹是曲线E，直线ｙ＝kx－1与曲线E交于A、B两点。如果且曲线E上存在点C，使求。
本小题主要考察双曲线的定义和性质、直线与双曲线的关系、点到直线的距离等知识及解析几何的基本思想、方法和综合解决问题的能力。
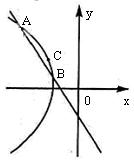
解析：由双曲线的定义可知，曲线
是以
为焦点的双曲线的左支，
且
，易知
故曲线的方程为
设
，由题意建立方程组
消去
，得
又已知直线与双曲线左支交于两点
，有
解得
又∵ 
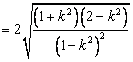
依题意得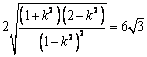 
整理后得 
∴
或
但 ∴
故直线
的方程为
设
，由已知
，得
∴
，
又
，
∴点
将点
的坐标代入曲线的方程，得
得
，但当
时，所得的点在双曲线的右支上，不合题意
∴
，点的坐标为
到的距离为
∴
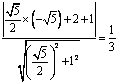
的面积