如图，PA切圆O于点A，割线PBC交圆O于点B、C，∠APC的角平分线分别与AB、AC相交于点D、E，求证：
(1) AD＝AE；
(2) AD2＝DB·EC.
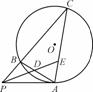
如图，PA切圆O于点A，割线PBC交圆O于点B、C，∠APC的角平分线分别与AB、AC相交于点D、E，求证：
(1) AD＝AE；
(2) AD2＝DB·EC.
证明：(1) ∠AED＝∠EPC＋∠C，∠ADE＝∠APD＋∠PAB.因为PE是∠APC的角平分线，所以∠EPC＝∠APD.又PA是圆O的切线，故∠C＝∠PAB.所以∠AED＝∠ADE.所以AD＝AE.
(2) 
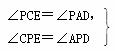
△PCE∽△PAD
＝
.
△PAE∽△PBD
＝
.又PA是切线，PBC是割线PA2＝PB·PC
又AD＝AE，所以AD2＝DB·EC.