如图1，抛物线y=ax2+2x+c与x轴交于A（﹣4，0），B（1，0）两点，过点B

如图1，抛物线y=ax²+2x+c与x轴交于A（﹣4，0），B（1，0）两点，过点B的直线y=kx+分别与y轴及抛物线交于点C，D．

（1）求直线和抛物线的表达式；

（2）动点P从点O出发，在x轴的负半轴上以每秒1个单位长度的速度向左匀速运动，设运动时间为t秒，当t为何值时，△PDC为直角三角形？请直接写出所有满足条件的t的值；

（3）如图2，将直线BD沿y轴向下平移4个单位后，与x轴，y轴分别交于E，F两点，在抛物线的对称轴上是否存在点M，在直线EF上是否存在点N，使DM+MN的值最小？若存在，求出其最小值及点M，N的坐标；若不存在，请说明理由．

解：（1）把A（﹣4，0），B（1，0）代入y=ax²+2x+c，得

，

解得：，

∴抛物线解析式为：y=，

∵过点B的直线y=kx+，

∴代入（1，0），得：k=﹣，

∴BD解析式为y=﹣；

（2）由得交点坐标为D（﹣5，4），

如图1，过D作DE⊥x轴于点E，作DF⊥y轴于点F，

当P₁D⊥P₁C时，△P₁DC为直角三角形，

则△DEP₁∽△P₁OC，

∴=，即=，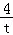

解得t=，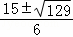

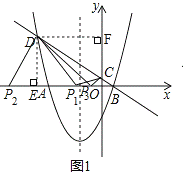
当P₂D⊥DC于点D时，△P₂DC为直角三角形

由△P₂DB∽△DEB得=，

即=，

解得：t=；

当P₃C⊥DC时，△DFC∽△COP₃，

∴=，即=，

解得：t=，

∴t的值为、、．

（3）由已知直线EF解析式为：y=﹣x﹣，

在抛物线上取点D的对称点D′，过点D′作D′N⊥EF于点N，交抛物线对称轴于点M

过点N作NH⊥DD′于点H，此时，DM+MN=D′N最小．

则△EOF∽△NHD′

设点N坐标为（a，﹣），

∴=，即=，

解得：a=﹣2，

则N点坐标为（﹣2，﹣2），

求得直线ND′的解析式为y=x+1，

当x=﹣时，y=﹣，

∴M点坐标为（﹣，﹣），

此时，DM+MN的值最小为==2．

【点评】本题是二次函数和几何问题综合题，应用了二次函数性质以及转化的数学思想、分类讨论思想．解题时注意数形结合．