 轴交于C、D两点,圆心A的坐标为(1,0),⊙A的半径为
轴交于C、D两点,圆心A的坐标为(1,0),⊙A的半径为 ,过点C作⊙A的切线交
,过点C作⊙A的切线交 轴于点B(-4,0).
轴于点B(-4,0).(1)求切线BC的解析式;
(2)若点P是第一象限内⊙A上的一点,过点P作⊙A的切线与直线BC相交于点G,且∠CGP=120°,求点G的坐标.

 轴交于C、D两点,圆心A的坐标为(1,0),⊙A的半径为
轴交于C、D两点,圆心A的坐标为(1,0),⊙A的半径为 ,过点C作⊙A的切线交
,过点C作⊙A的切线交 轴于点B(-4,0).
轴于点B(-4,0).


 ,OA="1" ,则OC=2
,OA="1" ,则OC=2 ,它过点C(0,2),B(−4,0),则有
,它过点C(0,2),B(−4,0),则有 解之得
解之得
 ……………………….(2分)
……………………….(2分) 轴,
轴, a + 2
a + 2  ×1200=600 ……………………….(3分)
×1200=600 ……………………….(3分)
 ∴AG =
∴AG = ……………………….(4分)
……………………….(4分) a+ 2
a+ 2 
 +
+ =
=
 +
+ =
=
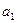 =
= ,
, = −
= − (舍去) ……………………….(5分)
(舍去) ……………………….(5分)  ,
, + 2 ) ……………………….(6分) 解析:
+ 2 ) ……………………….(6分) 解析: