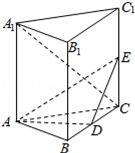
已知三棱柱ABC﹣A1B1C1，侧棱AA1垂直于底面ABC，AB=BC=AA1=4，D为BC的中点，
（1）若E为棱CC1的中点，求证：DE⊥A1C；
（2）若E为棱CC1上异于端点的任意一点，设CE与平面ADE所成角为α，求满足 时,求CE的长．
已知三棱柱ABC﹣A1B1C1，侧棱AA1垂直于底面ABC，AB=BC=AA1=4，D为BC的中点，
（1）若E为棱CC1的中点，求证：DE⊥A1C；
（2）若E为棱CC1上异于端点的任意一点，设CE与平面ADE所成角为α，求满足 时,求CE的长．
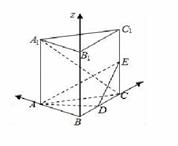解：（1）以B为原点，BC，BA，BB1所在直线分别为x轴，y轴，z轴，建立空间直角坐标系，……2分
∵AB=BC=AA1=4，D为BC的中点，E为棱CC1的中点，
∴D（2，0，0），E（4，0，2），A1（0，4，4），C（4，0，0），
=（2，0，2），
=（4，-4，-4），
=0+8﹣8=0，
∴DE⊥A1C． ………5分
（2）设E（4，0，t），0≤t≤4，
=（0，0，t），A（0，4，0），
=（2，-4，0），
=（4，-4，t），
设平面ADE的法向量
=（x，y，z），
则,
，取x=2，得=（2，1，﹣
）， ………8分
设CE与平面ADE所成角为α，满足sinα=
，∴
=
=
，
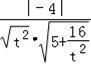解得t=3或t=﹣3（舍），∴CE=3 ………12分