已知椭圆![]()
![]() 的两个焦点分别为
的两个焦点分别为![]() ,
,![]() ,离心率为
,离心率为![]() ,过
,过![]() 的直线
的直线![]() 与椭圆
与椭圆![]() 交于
交于![]() ,
,![]() 两点,且△
两点,且△![]() 的周长为
的周长为![]() .
.
(Ⅰ)求椭圆![]() 的方程;
的方程;
(Ⅱ)过原点![]() 的两条互相垂直的射线与椭圆
的两条互相垂直的射线与椭圆![]() 分别交于
分别交于![]() ,
,![]() 两点,证明:点
两点,证明:点![]() 到直线
到直线![]() 的距离为定值,并求出这个定值.
的距离为定值,并求出这个定值.
已知椭圆![]()
![]() 的两个焦点分别为
的两个焦点分别为![]() ,
,![]() ,离心率为
,离心率为![]() ,过
,过![]() 的直线
的直线![]() 与椭圆
与椭圆![]() 交于
交于![]() ,
,![]() 两点,且△
两点,且△![]() 的周长为
的周长为![]() .
.
(Ⅰ)求椭圆![]() 的方程;
的方程;
(Ⅱ)过原点![]() 的两条互相垂直的射线与椭圆
的两条互相垂直的射线与椭圆![]() 分别交于
分别交于![]() ,
,![]() 两点,证明:点
两点,证明:点![]() 到直线
到直线![]() 的距离为定值,并求出这个定值.
的距离为定值,并求出这个定值.
解:(I)由题意知,![]() ,所以
,所以![]() .
.
因为![]()
所以![]() ,
,
所以![]() .
.
所以椭圆![]() 的方程为
的方程为![]() .
.
(II)由题意,当直线![]() 的斜率不存在,此时可设
的斜率不存在,此时可设![]() ,
,![]() .
.
又![]() ,
,![]() 两点在椭圆
两点在椭圆![]() 上,
上,
所以![]() ,
,![]() .
.
所以点![]() 到直线
到直线![]() 的距离
的距离![]() .
.
当直线![]() 的斜率存在时,设直线
的斜率存在时,设直线![]() 的方程为
的方程为![]() .
.
由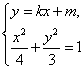 消去
消去![]() 得
得
![]() .
.
由已知![]() .
.
设![]() ,
,![]() .
.
所以![]() ,
,![]() .
.
因为![]() ,
,
所以![]() .
.
所以![]() .
.
即.
所以![]() .
.
整理得![]() ,满足
,满足![]() .
.
所以点![]() 到直线
到直线![]() 的距离
的距离
![]() 为定值.
为定值.