解法一：
由题设可知CG、CB、CD两两垂直,由此可建立空间直角坐标系,用向量法求解,即求出过B垂直于平面EFG的向量,它的模长即为点B到平面EFG的距离.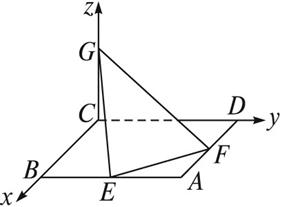
如图所示,以C为原点,CB、CD、CG所在直线分别为x、y、z轴建立空间直角坐标系C—xyz.
由题意知C(0,0,0),A(4,4,0),B(4,0,0),D(0,4,0),E(4,2,0),F(2,4,0),G(0,0,2).
=(0,2,0),
=(-2,4,0),
=(-4,0,2),
=(4,2,-2),
=(-2,2,0).
设向量
⊥平面GEF,垂足为M,则M、G、E、F四点共面,
故存在实数x,y,z,使
即
=x(0,2,0)+y(-2,4,0)+z(-4,0,2)
=(-2y-4z,2x+4y,2z).
由BM⊥平面GEF,得
于是
即
即
解得
∴
∴
即点B到平面GEF的距离为
.
解法二：利用BE在平面EFG的法向量n
上的射影求点B到平面EFG的距离,即d=
建立如解法一中图所示的坐标系,同解法一得
=(0,2,0),
=(4,2,-2),
=(-2,2,0).
设平面GEF的法向量为n
=(x,y,z),则有
令x=1,则y=1,z=3,∴n
=(1,1,3).点B到平面GEF的距离为
绿色通道：
用向量法求点到平面的距离,垂线段常常不必作出来,只需设出垂线段对应的向量或平面的法向量,利用向量垂直的条件转化为解方程组求其法向量.