(1)求数列{bn}的通项公式bn;
(2)设数列{an}的通项an=loga(1+
)(其中a＞0且a≠1)，记Sn是数列{an}的前n项和.试比较Sn与
logabn+1的大小，并证明你的结论.
(1)求数列{bn}的通项公式bn;
(2)设数列{an}的通项an=loga(1+)(其中a＞0且a≠1)，记Sn是数列{an}的前n项和.试比较Sn与logabn+1的大小，并证明你的结论.
(1)解：设数列{bn}的公差为d,由题意得
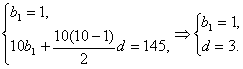∴bn=3n-2.
(2)证明：由bn=3n-2知
Sn=loga(1+1)+loga(1+)+…+loga(1+
)=loga［(1+1)(1+
)…+
)］,
而
logabn+1=loga
,于是，比较Sn与
logabn+1的大小比较(1+1)(1+
)…(1+
)与
的大小.
取n=1，有(1+1)=
；
取n=2，有(1+1)(1+
）＞
.
推测：(1+1)(1+
)…(1+
0＞
①
(Ⅰ)当n=1时，已验证①式成立.
(Ⅱ)假设n=k(k≥1)时①式成立，即(1+1)(1+
)…+
)＞
.
则当n=k+1时，(1+1)(1+
)…(1+
)［1+
］＞
(1+
)
=
.∵(
)3-(
)3
=
＞0,
∴
(3k+2)＞
=
.
从而(1+1)(1+
)…(1+
)(1+
)＞
，即当n=k+1时，①式成立.由(Ⅰ)(Ⅱ)知，①式对任意正整数n都成立.
于是，当a＞1时，Sn＞
logabn+1,当0＜a＜1时，Sn＜
logabn+1.