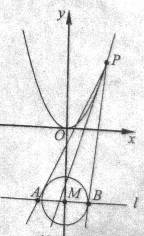
（本小题满分15分）如图，设P是抛物线
：
上的动点。过点
做圆
的两条切线，交直线
：
于
两点。
（Ⅰ）求的圆心
到抛物线 
准线的距离。
（Ⅱ）是否存在点，使线段
被抛物线在点处得切线平分，若存在，求出点的坐标；若不存在，请说明理由。
（本小题满分15分）如图，设P是抛物线：上的动点。过点做圆的两条切线，交直线：于两点。
（Ⅰ）求的圆心到抛物线 准线的距离。
（Ⅱ）是否存在点，使线段被抛物线在点处得切线平分，若存在，求出点的坐标；若不存在，请说明理由。
本题主要考查抛物线几何性质，直线与抛物线、直线与圆的位置关系，同时考查解析几何的基本思想方法和运算求解能力。满分15分。
（Ⅰ）解：因为抛物线C1的准线方程为：
所以圆心M到抛物线C1准线的距离为：
（Ⅱ）解：设点P的坐标为
，抛物线C1在点P处的切线交直线
于点D。
再设A，B，D的横坐标分别为
过点
的抛物线C1的切线方程为：
（1）
当
时，过点P（1，1）与圆C2的切线PA为：
可得
当
时，过点P（—1，1）与圆C2的切线PA为：
可得
所以
设切线PA，PB的斜率为
，则
（2）
（3）
将
分别代入（1），（2），（3）得
从而
又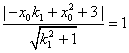
即
同理，
所以是方程
的两个不相等的根，从而
因为
所以
从而
进而得
综上所述，存在点P满足题意，点P的坐标为