=1(a＞b＞0)过点(1,
),且离心率e=
.(1)求椭圆方程；
(2)若直线l:y=kx+m(k≠0)与椭圆交于不同的两点M、N，且线段MN的垂直平分线过定点G(
,0),求k的取值范围.
=1(a＞b＞0)过点(1,),且离心率e=.(1)求椭圆方程；
(2)若直线l:y=kx+m(k≠0)与椭圆交于不同的两点M、N，且线段MN的垂直平分线过定点G(,0),求k的取值范围.
.∴=.∴a=2c.∴b2=a2-c2=3c2.∴椭圆方程为=1.
又点(1,
)在椭圆上,∴
+
=1.∴c2=1.∴椭圆的方程为
+
=1.
(2)设M(x1,y1),N(x2,y2).由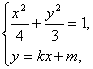
消去y并整理得(3+4k2)x2+8kmx+4m2-12=0.
∵直线y=kx+m与椭圆有两个交点,Δ=(8km)2-4(3+4k2)(4m2-12)＞0,即m2＜4k2+3.
又x1+x2=
,∴MN中点P的坐标为(
,
).
设MN的垂直平分线l′方程:y=
(x
),∵P在l′上,∴
=
(
),
即4k2+8km+3=0.∴m=
(4k2+3).
将上式代入得
＜4k2+3,∴k2＞
,即k＞
或k＜
.
∴k的取值范围为(-∞,
)∪(
,+∞).