已知g（x）为函数f（x）=2ax3﹣3ax2﹣12ax（a≠0）的导函数，则它们的图象可能是（ ）
A．
B．
C．
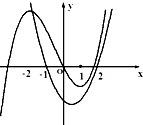D．
已知g（x）为函数f（x）=2ax3﹣3ax2﹣12ax（a≠0）的导函数，则它们的图象可能是（ ）
A． B． C． D．
A【分析】利用导数与函数之间的关系．把握住导数的正负确定出函数的单调区间，根据变化趋势选出恰当的图象．确定出答案．
【解答】解：∵f（x）=2ax3﹣3ax2﹣12ax（a≠0），
∴g（x）=f′（x）=6ax2﹣6ax﹣12a=6a
﹣
，
对称轴x=
，而f′（﹣1）=f′（2）=0，
根据f′（x）＞0时，y=f（x）递增；f′（x）＜0时，y=f（x）递减可得．
①中函数的图象的增减趋势与导函数的正负区间是吻合的，可能正确；
而②④中的对称轴不是，③中函数的图象的增减趋势与导函数的正负区间不吻合，故错误，
故选：A．
【点评】本题考查函数与其导函数的关系，函数的递增区间即为导函数为正的区间，函数的递减区间即为导函数为负的区间，根据这个依赖性可以确定出函数图形吻合的是哪一个．