
【小题1】求CD的长及∠1的度数;
【小题2】设DE = x,△GEF与梯形ABCD重叠部分的面积为y.
 求y与x之间的函数关系式,并求x为何值时,y的值最大?最大值是多少?
求y与x之间的函数关系式,并求x为何值时,y的值最大?最大值是多少?【小题3】当点G刚好落在线段BC上时,如图②,若此时将所得到的△EFG沿直线CB向左平移,速度为每秒1个单位,当E点移动到线段AB上时运动停止.设平移时间为t(秒),在平移过程中是否存在某一时刻t,使得△ABE为等腰三角形?若存在,求出t的值;若不存在,请说明理由

 求y与x之间的函数关系式,并求x为何值时,y的值最大?最大值是多少?
求y与x之间的函数关系式,并求x为何值时,y的值最大?最大值是多少? ∠1=30°
∠1=30°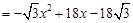
 时,y的值最大,y的最大值为
时,y的值最大,y的最大值为

 解析:
解析: =
=
 (2分)
(2分)
 EG=
EG= x
x
 (5分)
(5分)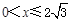 时
时
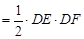


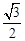 >0,对称轴为y轴
>0,对称轴为y轴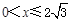 ,y随x的增大而增大
,y随x的增大而增大 时,
时, =
= (6分)
(6分) <x≤
<x≤ 时,设FG,EG分别交BC于点M、N
时,设FG,EG分别交BC于点M、N ,NE=2
,NE=2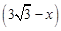
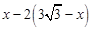 =
=
 =
=




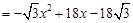 (7分)
(7分) ,对称轴为直线
,对称轴为直线
 <x≤
<x≤ 时,y有最大值
时,y有最大值 时,
时, =
= (8分)
(8分) <
<
 时,y的值最大,y的最大值为
时,y的值最大,y的最大值为 (9分)
(9分)
 (12分)
(12分)