如图,在四棱锥B-AA1C1C中,AA1C1C是边长为4的正方形,平面ABC⊥平面AA1C1C,AB=3,BC=5.
(Ⅰ)求证:AA1⊥平面ABC;
(Ⅱ)求二面角A1-BC1-C的余弦值;
(![]() Ⅲ)证明:在线段上
Ⅲ)证明:在线段上![]() 存在点D,使得AD⊥A1B,并求
存在点D,使得AD⊥A1B,并求![]() 的值.
的值.
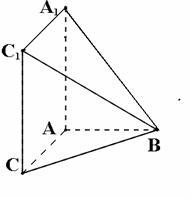
如图,在四棱锥B-AA1C1C中,AA1C1C是边长为4的正方形,平面ABC⊥平面AA1C1C,AB=3,BC=5.
(Ⅰ)求证:AA1⊥平面ABC;
(Ⅱ)求二面角A1-BC1-C的余弦值;
(![]() Ⅲ)证明:在线段上
Ⅲ)证明:在线段上![]() 存在点D,使得AD⊥A1B,并求
存在点D,使得AD⊥A1B,并求![]() 的值.
的值.

(I)因为AA1C1C为正方形,所以AA1 ⊥AC.
因为平面ABC⊥平面AA1C1C,且AA1垂直于这两个平面的交线AC,所以AA1⊥平面ABC.
(II)由(I)知AA1 ⊥AC,AA1 ⊥AB. 由题知AB=3,BC=5,AC=4,所以AB⊥AC. 如图,以A为原点建立空间直角坐标系A-![]() ,则B(0,3,0),A1(0,0,4),B1(0,3,4),C1(4,0,4),
,则B(0,3,0),A1(0,0,4),B1(0,3,4),C1(4,0,4),
设平面A1BC1的法向量为![]() ,则
,则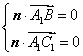 ,即
,即![]() ,
,
令![]() ,则
,则![]() ,
,![]() ,所以
,所以![]() .
.
同理可得,平面BCC1的法向量为![]() ,所以
,所以![]() . 由题知二面角A1-BC1-C为钝角,所以二面角A1-BC1-C的余弦值为
. 由题知二面角A1-BC1-C为钝角,所以二面角A1-BC1-C的余弦值为![]() .
.
(III)设D![]() 是直线BC1上一点,且
是直线BC1上一点,且![]() . 所以
. 所以![]() .解得
.解得![]() ,
,![]() ,
,![]() .
.
所以![]() .
.
由![]() ,即
,即![]() .解得
.解得![]() .
.
因为![]() ,所以在线段BC1上存在点D,
,所以在线段BC1上存在点D,
使得AD⊥A1B. 此时,![]() .
.