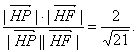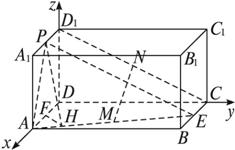
(1)求证：MN∥面ADD1A1；
(2)求二面角PA-E-D的余弦值.
(1)求证：MN∥面ADD1A1；
(2)求二面角PA-E-D的余弦值.
（1）证明
:如图，以D为原点，DA、DC、DD1所在直线分别为x轴、y轴、z轴建立直角坐标系.
则A（a,0,0）,B(a,2a,0),C(0,2a,0),A1(a,0,a),D1(0,0,a).
因为E、P、M、N分别为BC、A1D1、AE、CD1的中点,
所以E（
,2a,0）,P(
,0,a),M(
a,a,0),N(0,a,
).
=(-
a,0,
),取n
因为
·n
⊥n.又MN
平面ADD1A1，所以MN∥平面ADD1A1.
（2）解：
过P作PH⊥AE,交AE于H，取AD的中点F，则F（
,0,0）,设H（x,y,0）,则
=（
-x,-y,a）,
=(
-x,-y,0).又
=（-
,2a,0）,
由
·
=0，及H在直线AE上可得
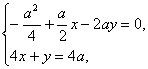解得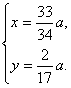
所以
=（
a,a）,
=(
a,0).
所以
·
=0，即
⊥
.
所以
与
所夹的角等于二面角P-AE-D的平面角,其余弦值为cos〈
,
〉=