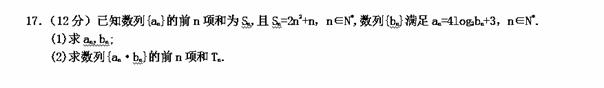
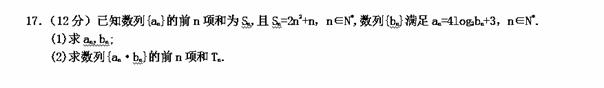
(1)由Sn=2n2+n,可得
当n≥2时，
an=Sn-Sn-1=(2n2+n)-[2(n-1)2+(n-1)]=4n-1,
当n=1时，a1=3符合上式，所以an=4n-1(n∈N*).
由an=4log2bn+3，可得4n-1=4log2bn+3,
解得bn=2n-1(n∈N*).
(2)anbn=(4n-1)·2n-1,
∴Tn=3+7×21+11×22+15×23+…+(4n-1)×2n-1， ①
2Tn=3×21+7×22+11×23+15×24+…+(4n-1)×2n， ②
①-②可得
-Tn=3+4[21+22+23+24+…+2n-1]-(4n-1)×2n
=3+4×
-(4n-1)×2n
=-5+(5-4n)×2n,
∴Tn=5+(4n-5)×2n.