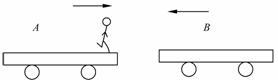
如图16所示,光滑水平面上A、B两小车质量都是M,A车头站立一质量为m的人,两车在同一直线上相向运动.为避免两车相撞,人从A车跃到B车上,最终A车停止运动,B车获得反向速度v0,试求:
(1)两小车和人组成的系统的初动量大小.
(2)为避免两车相撞,且要求人跳跃速度尽量小,则人跳上B车后,A车的速度多大?
 | |||
| |||
如图16所示,光滑水平面上A、B两小车质量都是M,A车头站立一质量为m的人,两车在同一直线上相向运动.为避免两车相撞,人从A车跃到B车上,最终A车停止运动,B车获得反向速度v0,试求:
(1)两小车和人组成的系统的初动量大小.
(2)为避免两车相撞,且要求人跳跃速度尽量小,则人跳上B车后,A车的速度多大?
 | |||
| |||
解析:(1)由动量守恒定律可知,系统的初动量大小为p=(M+m)v0.
(2)为避免两车发生碰撞,最终两车和人具有相同速度(设为v),则(M+m)v0=(2M+m)v,
解得v=(M+m)v0/(2M+m)