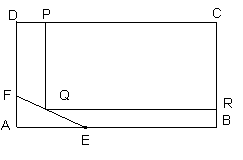
为了绿化城市，准备在如图所示的区域内修建一个矩形PQRC的草坪，且PQ∥BC,RQ⊥BC,另外△AEF的内部有一文物保护区不能占用，经测量AB=100m,BC=80m,AE=30m,AF=20m．
（1）求直线EF的方程．
（2）应如何设计才能使草坪的占地面积最大？
 |
为了绿化城市，准备在如图所示的区域内修建一个矩形PQRC的草坪，且PQ∥BC,RQ⊥BC,另外△AEF的内部有一文物保护区不能占用，经测量AB=100m,BC=80m,AE=30m,AF=20m．
（1）求直线EF的方程．
（2）应如何设计才能使草坪的占地面积最大？
|
（1）建立坐标系如图所示，在线段EF上任取一点Q，分别向BC，CD作垂线．
由题意，直线EF的方程为：
；
（2）设Q（x，20-
x），则矩形PQRC的面积为：S=（100-x）•[80-（20-x）]（其中0≤x≤30）；
化简，得S=-x2+
x+6000 （其中0≤x≤30）；
所以，当x=-
=5时，此时y=20-×5=
，即取点Q（5，）时，S有最大值，最大值为6016m2．