).(1)设x=x0是函数y=f(x)图象的一条对称轴,求g(x0)的值;
(2)求使函数h(x)=f(
)+g(
)(ω＞0)在区间［
,
］上是增函数的ω的最大值.
).(1)设x=x0是函数y=f(x)图象的一条对称轴,求g(x0)的值;
(2)求使函数h(x)=f()+g()(ω＞0)在区间［,］上是增函数的ω的最大值.
sin2x,因为x=x0是函数y=f(x)图象的一条对称轴,所以2x0=kπ+,k∈Z
g(x0)=［1+cos(2x0+)］=［1+cos(kπ+
)］,
当k为偶数时,g(x0)=
(1+cos
)=
;
当k为奇数时,g(x0)=
(1+cos
)=
.
(2)因为h(x)=(1+
sinωx)+
［1+cos(ωx+
)］
=
(sinωx+
cosωx-
sinωx)+
=
sin(ωx+
)+
,
当x∈［
,
］时,ωx+
∈［
+
,
+
］,
因为h(x)在［
,
］上是增函数,且ω＞0,
所以［
+
,
+
］
［
,
］,
即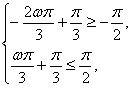
解得ω≤
.
所以ω的最大值为
.