(本小题满分12分)
|
(Ⅰ)求椭圆![]() 的方程;
的方程;
(Ⅱ)过点![]() (4,0)且不与坐标轴垂直的直线
(4,0)且不与坐标轴垂直的直线![]() 交椭圆
交椭圆![]() 于
于![]() 、
、![]() 两点,设点
两点,设点![]() 关于
关于![]() 轴的对称点为
轴的对称点为![]() .
.
(ⅰ)求证:直线![]() 过
过![]() 轴上一定点,并求出此定点坐标;
轴上一定点,并求出此定点坐标;
(ⅱ)求△![]() 面积的取值范围.
面积的取值范围.
(本小题满分12分)
|
(Ⅰ)求椭圆![]() 的方程;
的方程;
(Ⅱ)过点![]() (4,0)且不与坐标轴垂直的直线
(4,0)且不与坐标轴垂直的直线![]() 交椭圆
交椭圆![]() 于
于![]() 、
、![]() 两点,设点
两点,设点![]() 关于
关于![]() 轴的对称点为
轴的对称点为![]() .
.
(ⅰ)求证:直线![]() 过
过![]() 轴上一定点,并求出此定点坐标;
轴上一定点,并求出此定点坐标;
(ⅱ)求△![]() 面积的取值范围.
面积的取值范围.
解:(Ⅰ)因为椭圆![]() 的一个焦点是(1,0),所以半焦距
的一个焦点是(1,0),所以半焦距![]() =1.
=1.
因为椭圆两个焦点与短轴的一个端点构成等边三角形.
所以![]() ,解得
,解得![]() 所以椭圆的标准方程为
所以椭圆的标准方程为![]() . ……………4分
. ……………4分
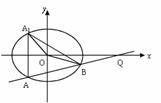 (Ⅱ)(i)设直线
(Ⅱ)(i)设直线![]() :
:![]() 与
与![]() 联立并消去
联立并消去![]() 得:
得:![]() .
.
记![]() ,
,![]() ,
,![]() ,
,
![]() . 由A关于
. 由A关于![]() 轴的对称点为
轴的对称点为![]() ,得
,得![]() ,根据题设条件设定点为
,根据题设条件设定点为![]() (
(![]() ,0),得
,0),得![]() ,即
,即![]() .所以
.所以![]()
![]()
即定点![]() (1 , 0). ……………8分
(1 , 0). ……………8分
(ii)由(i)中判别式![]() ,解得
,解得![]() . 可知直线
. 可知直线![]() 过定点
过定点![]() (1,0).
(1,0).
所以![]() 得
得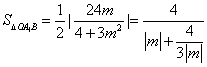 , 令
, 令![]() 记
记![]() ,得
,得![]() ,当
,当![]() 时,
时,![]() .
.
![]() 在
在![]() 上为增函数. 所以
上为增函数. 所以![]()
![]() ,
,
得![]() .故△OA1B的面积取值范围是
.故△OA1B的面积取值范围是![]() . ……………12分
. ……………12分