(本小题满分14分)
已知函数![]() ,且定义域为(0,2).
,且定义域为(0,2).
(1)求关于x的方程![]() +3在(0,2)上的解;
+3在(0,2)上的解;
(2)若![]() 是定义域(0,2)上的单调函数,求实数
是定义域(0,2)上的单调函数,求实数![]() 的取值范围;
的取值范围;
(3)若关于x的方程![]() 在(0,2)上有两个不同的解
在(0,2)上有两个不同的解![]() ,求k的取值范围。
,求k的取值范围。
(本小题满分14分)
已知函数![]() ,且定义域为(0,2).
,且定义域为(0,2).
(1)求关于x的方程![]() +3在(0,2)上的解;
+3在(0,2)上的解;
(2)若![]() 是定义域(0,2)上的单调函数,求实数
是定义域(0,2)上的单调函数,求实数![]() 的取值范围;
的取值范围;
(3)若关于x的方程![]() 在(0,2)上有两个不同的解
在(0,2)上有两个不同的解![]() ,求k的取值范围。
,求k的取值范围。
解(1)![]() ,
,![]() +3即
+3即![]()
当![]() 时,
时,![]() ,此时该方程无解. ……1分
,此时该方程无解. ……1分
当![]() 时,
时,![]() ,原方程等价于:
,原方程等价于:![]() 此时该方程的解为
此时该方程的解为![]() .
.
综上可知:方程![]() +3在(0,2)上的解为
+3在(0,2)上的解为![]() .……3分
.……3分
(2)![]()
![]() ,
,
![]() ………4分
………4分
![]() ,…………5分
,…………5分
可得:若![]() 是单调递增函数,则
是单调递增函数,则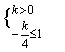
![]() …6分
…6分
若![]() 是单调递减函数,则
是单调递减函数,则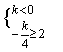
![]() ,………7分
,………7分
综上可知:![]() 是单调函数时
是单调函数时![]() 的取值范围为
的取值范围为![]() .…8分
.…8分
(2)[解法一]:当![]() 时,
时,![]() ,①
,①
当![]() 时,
时,![]() ,②
,②
若k=0则①无解,②的解为![]() 故
故![]() 不合题意。…………9分
不合题意。…………9分
若![]() 则①的解为
则①的解为![]() ,
,
(Ⅰ)当![]() 时,
时,![]() 时,方程②中
时,方程②中![]()
故方程②中一根在(1,2)内另一根不在(1,2)内,…………10分
设![]() ,而
,而![]() 则
则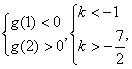 又
又![]() ,故
,故![]() ,………11分
,………11分
(Ⅱ)当![]() 时,即
时,即![]() 或
或![]() 0时,方程②在(1,2)须有两个不同解,…12分
0时,方程②在(1,2)须有两个不同解,…12分
而![]() ,知方程②必有负根,不合题意。……13分
,知方程②必有负根,不合题意。……13分
综上所述,![]() ………14分
………14分
[略解法二]![]() ,………9分
,………9分
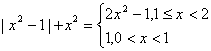 ,
,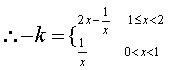 ………10分
………10分
分析函数的单调性及其取值情况易得解(用图象法做,必须画出草图,再用必要文字说明)……………13分
利用该分段函数的图象得![]() ……………………14分
……………………14分