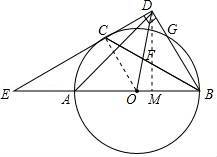
如图，AB为⊙O的直径，C，G是⊙O上两点，过点C的直线CD⊥BG于点D，交BA的延长线于点E，连接BC，交OD于点F，且BC平分∠ABD．
（1）求证：CD是⊙O的切线；
（2）若
=
，求∠E的度数；
（3）连结AD，在（2）的条件下，若CD=2
，求AD的长．
如图，AB为⊙O的直径，C，G是⊙O上两点，过点C的直线CD⊥BG于点D，交BA的延长线于点E，连接BC，交OD于点F，且BC平分∠ABD．
（1）求证：CD是⊙O的切线；
（2）若=，求∠E的度数；
（3）连结AD，在（2）的条件下，若CD=2，求AD的长．
证明：（1）连接OC，
∵OC=OB，BC平分∠ABD，
∴∠OCB=∠OBC，∠OBC=∠DBC，
∴∠DBC=∠OCB，
∴OC∥BD，
∴∠BDC=∠ECO，
∵CD⊥BD，
∴∠BDC=90°，
∴∠ECO=90°，
∵OC是⊙O的半径，
∴CD是⊙O的切线；
（2）由（1）知，
OC∥BD
，
∴∠OCF=∠DBF，∠COF=∠BDF，
∴△OCF∽△DBD，
∴
，
∵=，
∴
，
∵OC∥BD，
∴△EOC∽△EDB，
∴
，
∴
，
设OE=2a，EB=3a，
∴OB=a，
∴OC=a，
∵∠OCE=90°，OC=
OE，
∴∠E=30°；
（3）∵∠E=30°，∠BDE=90°，BC平分∠DBE，
∴∠EBD=60°，∠OBC=∠DBC=30°，
∵CD=2
，
∴BC=4，BD=6，
∵
，
∴OC=4，
作DM⊥AB于点M，
∴∠DBM=90°，
∵BD=6，∠DBM=60°，
∴BM=3，DM=3，
∵OC=4，
∴AB=8，
∴AM=5，
∵∠DMA=90°，DM=3，
∴AD=
=
．
